자료구조 정리
기본 자료구조 종류
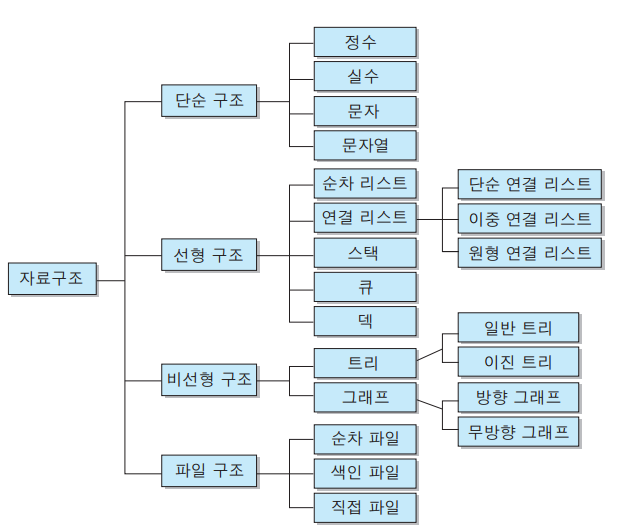
선형 자료구조 (linaer)
- 배열 (Array)
- 연결리스트 (Linked List)
- 스택 (Stack)
- 큐 (Queue)
비선형 자료구조 (non-linear)
- 트리 (Tree)
- 그래프 (Graph)

1. 배열
1) 정의
같은 자료형을 갖는 여러 데이터를 하나의 변수 이름으로 모아놓은 데이터의 집합체
2) 특징
- 논리적순서와 물리적 순서가 같다.
- 인덱스를 통해 직접적으로 원소에 접근한다.
- 삽입, 삭제 시 자료의 이동에 따른 오버헤드가 발생하기 때문에 삽입/삭제 연산이 빈번하게 일어나는 연산에서는 부적합하다.
2. 연결리스트
1) 정의
노드 (하나 이상의 데이터 필드와 하나 이상의 링크 필드로 구성)라는 저장구조를 이용해서 선형 리스트를 표현하는 방법
2) 특징
- 논리적순서와 물리적순서가 같지 않다.
- 링크 필드의 조정을 통해 배열보다 비교적 간단하게 삽입/삭제 연산을 할 수 있다.
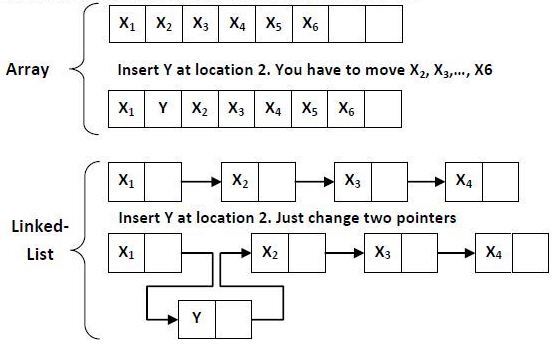
- 순차접근을 해야하기 때문에 검색시 배열보다는 효율이 떨어지는 편이다.
3) 종류
- 단일 연결리스트 (Singly Linked List) : 노드가 한방향으로만 갈 수 있음, 노드의 끝이 있음
- 이중 연결리스트 (Doubly Linked List) : 각 노드가 이전 노드, 다음 노드에 대해서 참조하는 형태의 연결 리스트
- 단일 연결 리스트 : 노드가 한방향으로만 갈 수 있음, 노드의 끝이 없어 양 노드의 끝이 처음으로 이어질 수 있음
- 이중 연결 리스트 : 노드가 양방향으로 갈 수 있음, 노드의 끝이 없어 양 노드의 끝이 처음으로 이어질 수 있음
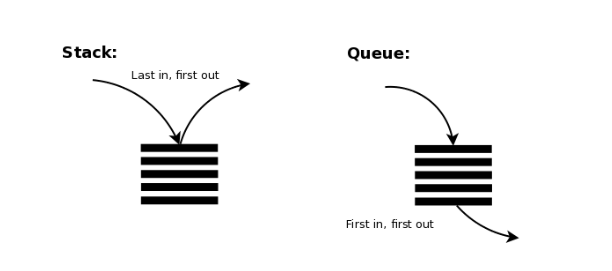
3. 스택
1) 정의
한쪽 끝에서만 데이터의 삽입과 삭제가 수행되는 선형 리스트
2) 특징
- 가장 늦게 들어간 데이터가 가장 먼저 나오는 후입선출 (LIFO) 의 형식을 가진다.
- 데이터를 삽입하는 push 연산과 데이터를 출력하는 pop 연산이 있다.
- TOP에서만 데이터의 삽입과 삭제가 수행된다.
4. 큐
1) 정의
한쪽 끝에서는 데이터의 삽입만 수행되고 다른 한쪽 끝에서는 삭제만 수행되는 선형 리스트
2) 특징
- 가장 먼저 들어간 데이터가 가장 먼저 나오는 선입선출 (FIFO) 의 형식을 가진다.
- 가장 앞부분을 front / head라고 하며, 가장 뒷부분을 rear / tail이라고 한다.
5-1. 트리

1) 정의
노드라는 정보 항목이 간선으로 연결되어 계층적인 구조를 표현하는 비선형 자료구조
2) 용어
- 서브 트리 (subtree) : 하나의 노드와 그 노드들의 자손들로 이루어진 트리
- 루트 노드(root) : 부모가 없는 노드로 트리는 하나의 루트 노드만을 가진다.
- 노드의 차수 (degree) : 하위 트리 갯수/간선수 (degree)로, 각 노드가 지닌 가지의 수를 말한다.
- 리프 노드(leaf node), 단말 노드 : 자식이 없는 노드를 말한다.
- 비단말노드 : 적어도 하나의 자식을 가지는 노드를 말한다.
- 부모 노드 (parent) :
- 자식 노드 (child) :
- 형제 노드 (sibling) : 같은 부모를 가지는 노드를 말한다.
- 후손(자손, descendent) :
- 조상(선조, ancestor) :
- 레벨 : 루트 노드로부터의 길이
- 높이/깊이 (height, depth) : 루트 노드에서 가장 깊숙히 있는 노드의 깊이로 '가장 마지막 레벨 + 1'로 구할 수 있다.
- 차수(degree) : 노드가 가지고 있는 자식 노드의 개수
- 숲
5-2. 이진트리

1) 정의
각 노드의 차수가 2이하(0,1,2)인 순서 트리
2) 특징
- 레벨 i에서의 최대 노드 개수: 2i
- 높이 h인 트리의 최대 노드 개수 : 2h - 1
- n0=n2+1 (n0: 단일 노드의 수, n2: 차수가 2인 노드의 수)
3) 종류
- 포화(perfect) 이진트리 : 모든 리프 노드의 레벨이 동일하고 모든 레벨이 가득 채워져 있는 이진 트리를 말한다.
- 완전(complete) 이진트리 : 부모, 왼쪽 자식, 오른쪽 자식 순으로 채워지는 트리를 말하며, 마지막 레벨을 제외하고 모든 노드가 가득 차 있어야 한다. 또한, 마지막 레벨의 노드도 중간에 빈 곳 없이 왼쪽으로 몰려 있어야 한다.
- 전이진트리 (full) : 노드차수가 0 이거나 2인 이진트리를 말하며 균형 이진트리 (balanced)라고도 한다.

6. 그래프
1) 정의
G = (V, E)
V : 정점(연결해야 할 대상)의 집합
E : 간선(연결선)의 집합
2) 종류
방향성의 위치에 따라 무방향 그래프와 방향그래프로 구분한다.
무방향 그래프 (undirected)
(1,0) = (0,1)
방향이 없기 때문에 어디든 같아 이런식으로() 표현한다.
방향그래프 (directed)
<1,2> =/= <2,1>
방향이 있기 때문에 이렇게<> 표현하며 값이 맞지 않기 때문에 둘은 다르다.
또한 가중치가 있을 경우 가중그래프(weighted)라고 한다.
3) 용어
- 인접(adjacent)
- 부수(incident)
- 부분 그래프 (subgraph)
- 경로(path)
- 경로의 길이(length)
- 차수(degree)
방향 그래프 -> 진입 차수(in-degree), 진출 지수(out-degree)
- 단순 경로(simple path)
- 사이클(cycle)
- 루프(loop)
- 연결(connected)
방향그래프 -> 강력 연결(strongly-connected), 약하게 연결(weakly-connected)
4) 그래프의 구현
인접행렬 (adjacency matrix) : 이중배열을 사용해서 구현
만약 가중치가 없는 그래프일 경우 선이 있냐 없냐인 1,0으로 구성되어 표현됨
인접리스트 (adjacency list) : linkedList 사용해서 구현